Im März 2021 wurde von KPMG eine Studie zum Thema Insurance Pricing veröffentlicht, die es den Versicherungsunternehmen ermöglicht ihren Reifegrad hinsichtlich Pricing am österreichischen Markt zu vergleichen (https://info.kpmg.at/InsurancePricingStudie/). Insgesamt 15 österreichische Versicherungsunternehmen beantworteten Fragen rund um die Tarifierung, die Aufstellung ihrer Pricing Aktuariate und Prozessstrukturen.
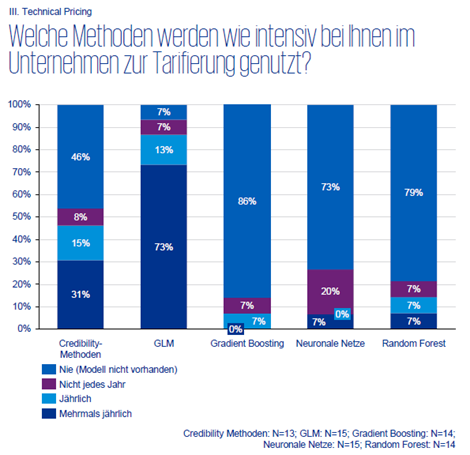
Vor allem in einem Punkt sind sich die Non-Life Pricing Aktuar:innen vorerst einig, und zwar bei der Methodik der Preisberechnung. Wie in der Grafik unterhalb ersichtlich ist, werden in der Praxis am intensivsten GLMs (Generalized Linear Models) angewendet – Machine Learning Techniken wie Gradient Boosting, Neuronale Netze und Random Forests werden nur selten zur Tarifierung genützt.
GLM ist, wie der Name schon sagt, eine Verallgemeinerung des linearen Regressionsmodells. Es gibt eine Zielgröße oder auch abhängige Variable, wie zum Beispiel die Schadenfrequenz, und diverse erklärende Variablen (Alter, Automarke, etc.) deren Zusammenhang mit der Zielgröße aufgezeigt werden soll. Das Ziel eines GLM ist die abhängige Variable möglichst gut zu prognostizieren und Zusammenhänge zu verstehen. Der Vorteil von GLM liegt in der einfachen Interpretierbarkeit aufgrund seiner multiplikativen Struktur. Die Flexibilität ist jedoch eingeschränkt, da vom Modellierer Verteilungsannahmen getroffen werden müssen und damit komplexe Zusammenhänge eventuell übersehen werden.
Bei entscheidungsbaumbasierten Methoden (Supervised Machine Learning) wie Gradient Boosting oder Random Forests wird auf Basis eines Datensatzes mit einer bekannten Zielvariable ein Modell mit Hilfe von Einflussvariablen aufgebaut, um die Zielvariable vorhersagen zu können. Der wesentliche Vorteil ist jedoch, dass keine Verteilungsannahmen getroffen und nicht-lineare Beziehungen automatisch erfasst werden. Diese größere Flexibilität kann damit zu besseren Modellvorhersagen führen.
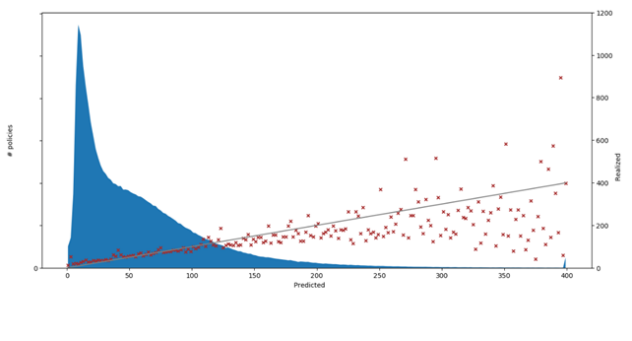
Als Beispiel für die Prognosefähigkeit wird in der folgenden Grafik das Resultat eines GBM-Modelles für den Schadenbedarf (= Schadenfrequenz * Durchschnittsschaden) eines Motor-Portfolios dargestellt. Auf der X-Achse sehen wir die prognostizierten Werte und auf der rechten Y-Achse die Echtwerte. Vorhersagen, die die Echtwerte exakt getroffen haben, liegen direkt auf der grauen Linie.
Obwohl wir in der Grafik den Zusammenhang der Vorhersagen mit den Echtwerten visuell leicht erkennen können, gibt es eine Vielzahl an Metriken mit denen die Prognosegüte eines Modelles beschrieben werden kann. Zum Beispiel kann ein Korrelationskoeffizient von 0.034 für das hier verwendete GBM-Modell errechnet werden – dazu im Vergleich ergibt dieser Koeffizient 0.030 für ein GLM-Modell auf demselben Datensatz. In diesem Fall besteht also beim GBM ein höherer Zusammenhang zwischen Prognose und Echtwerten als beim GLM.
Es ist relativ einfach ein GLM in seiner Prognosefähigkeit mittels Machine Learning (ML) Methoden zu schlagen, trotzdem werden in der Praxis GLMs bevorzugt. Warum ist das so?
Oft werden als Gründe fehlende Rechenleistung, mangelndes Wissen, Mangel an Daten und Probleme mit dem Datenschutz genannt. Denkbar wäre, dass es auch am Vertrauen in die neuen Algorithmen scheitert. Dabei sind diese nicht immer neu. Die dahinterliegenden mathematischen Prinzipien gibt es meistens schon Jahrzehnte, doch erst durch die Verbesserung der Rechenleistung ist die Verwendung von komplexeren Modellen möglich geworden.
Aktuar:innen sind meistens an der besten Prognose interessiert, jedoch auf einem Komplexitätsniveau, das immer noch klar und verständlich erklärt werden kann. Tarifentscheidungen werden nicht nur von Mathematiker:innen alleine getroffen. Die Preissetzung ist ein Projekt mit vielen Beteiligten aus verschiedenen Bereichen und damit eine interdisziplinäre Zusammenarbeit.
ML-Algorithmen sind häufig um einiges schwieriger zu erklären und opfern deshalb ein Stück Verständlichkeit gegen eine Verbesserung des Prognoseergebnisses.
Bei vielen anderen Aufgabenstellungen jedoch, wie zum Beispiel bei der Modellierung von Kundensegmenten oder bei Betrugserkennungen ist es nicht wichtig warum ein Modell ein gewisses Ergebnis liefert – es zählt einzig und allein die Genauigkeit. Genauso gibt es auch in der Tarifierung Anwendungsgebiete in denen ML-Learning Techniken verwendet werden können, wie zum Beispiel bei der Datenbereinigung oder auch bei der Modellierung der Nachfrage. In einem Nachfragemodell oder demand model wird geschätzt, wieviel ein Kunde oder eine Kundin in der aktuellen Marktumgebung für ein Versicherungsprodukt bezahlen würde. Diese Art von Modell wird üblicherweise öfter aktualisiert als ein Risikomodell, da auch die Nachfrage in einem dynamischen Markt volatiler ist als das Risiko. Ein automatisierter Modellierungsprozess kann hier Zeit ersparen und lässt deshalb verstärkt zu ML-Methoden greifen.
Weiters können ML-Techniken auch bei der Validierung von Risikomodellen hilfreich sein oder auch bei der Entdeckung von Interaktionen.
Zusammenfassend kann gesagt werden, dass ML-Algorithmen immer öfter als zusätzliches Hilfsmittel verwendet werden, aufgrund der geringeren Transparenz werden sie aber wohl auch in unmittelbarer Zukunft die GLMs als Tarifierungsmethodik nicht völlig ablösen.



